Atari Computer
Welches System? -
Hardware -
Software -
Emulatoren -
MausNet
Programmieren
Verweise
Über
|
Hauptseite - Welches System? - Hardware - Software - Emulatoren - |
Internet MausNet Programmieren Verweise Über |
Die Listen haben den Nachteil, das eine Suche nach einem bestimmten Element immer der Reihe nach jedes Element der Liste vergelichen muß, also im ungünstigsten Fall die Liste komplett durchwandert. Die Suche kann stark beschleunigt werden, wenn jeder Knoten zwei Zeiger hat. Ein Zeiger zeigt auf Elemente, die kleiner sind und ein Zeiger zeigt auf Elemente, die größer sind.
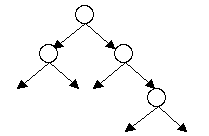
Geht man von der Wurzel des Baums einen Knoten weiter, so kann dieser Knoten mit seinen Unterknoten wieder als ein Teilbaum betrachtet werden. Deshalb lassen sich einige Operationen sehr einfach relursiv beschreiben.
Das Einfügen ein es neuen Elements geht wie folgt:
Auch das Suchen läßt sich rekursiv leicht beschreiben:
Für das komplette Durchwandern des Baums gibt es drei verschiedenen Möglichkeiten, die sich in der Reihenfolgem, in der die einzelnen Knoten bearbeitet werden, unterscheiden
Das Entfernen eines Knoten ist allerdings aufwendiger, da zwei Teilbäume zu einem Teilbaum vereinigt werden müssen. Wenn einer der zwei Teilbäume des zu entfernenden Knotens leer ist, ist das Löschen einfach. Der nicht leere Teilbaum ersetzt den zu löschenden Knoten. Seind beide Teilbäume nicht leer, kann der folgende Algorithmus benutzt werden:

Alternativ kann natürlich auch der rechte Teilbaum in den linken eingebaut werden. Das zu löschende Element wird dann durch den linken Teilbaum ersetzt.
Beispielcode

|
English version not yet available. |